Batch 3 - Class 259 - Probability in Gaming - Monopoly, Pagerank
(zoom)
Pre-Class Exercise
- Place 52 cards from a deck face down in a line. Turn the first card, and then move number of cards further equivalent to the face value of the opened card. Now open the card that you land on and continue the same process till you get to the end of the deck (meaning the last card, beyond which when you try to move by face value of the card, you would run out of cards). Mark the last card that was opened. Now, if I do the same process, starting not from the first card but any of the next 9 cards (card numbers 2-10), what are the chances of my last card being the same as yours?
- Answer: about 80%. Note that on each step there is a 1/13 chance (actually more, since you may have two of your opened cards in my next 13 cards on an average) that I land up on one of your prior opened cards, and then I follow the same journey. In a 52 card stretch, this opportunity may arise about 7 times. That combines to give fairly high chances that one would land up on the same card at least once.
- Roughly 2/13+11/13*(2/13+11/13*(2/13+11/13*(2/13+11/13*(2/13+11/13*(2/13+11/13*(2/13)))))) ~ 69% (actual probability is around 80%)
Attendance Advay, Raghav, Angad, Ayush, Aneesh, Shikhar, SiddharthT, Harshiet, SiddhantJ, Anshi, Kabir, Rohan, Aashvi, Mihir, Rhea, Vansh, Vivaan, Anishka, Arjun, Aarkin, Kushagra, Rehan, Arnav
Class Notes:
Review of Last Class. Key concepts
- Independent events: History does not influence the future outcomes. Eg: roll of dice
- Probability: For independent events, probability of successive outcomes is product of individual probabilities
- Expected outcomes: Win/loss multiplied by respective probabilities
Casino Games
- House Advantage in gambling - 5.26% for roulette; ~1-2% in blackjack
Bookies
- Don't take a position but manage bets to make fee income
Today: What if the events are not independent? History affects the future?
Simple Chair Game
Lets have two chairs A and B. A person starts sitting at either of those chairs, and on each time interval, she stays or swaps chairs on basis of the following rules:
- If she is sitting on chair A, then she swaps with probability 1/2
- If she is sitting on chair B, then she swaps with probability 1/4 (simulate with two coins)
After a long series of events, what is the probability of us finding her on chair A versus B?
- Let us run this by simulation - we will essentially have someone sit on the chair, and get them to move around for 30 turns, and see where we are landing
- Does this change if the starting seat is changed?
- Look at total chances, as well as chances ignoring the first 10 turns
- Answer: In this case, chances of finding the person on chair A is 1/3, and chances of finding the person on chair B is 2/3
Rainy Day
Suppose I told you that in a year, chances of a day being rainy is 0.5 and chances of a day being sunny is 0.5. It is raining today, what are the chances it will rain tomorrow?
- Instinctive answer of kids can be 0.5 - ask them if that is how they have normally seen it work. Or are there "rainy seasons" and "sunny seasons"?
- Note that the above is true only if the chances are independent of history. What if they are not?
- Lets try this - let us say that if today is rainy, then chances of tomorrow being rainy is 5/6. Similarly, if today is sunny, chances of tomorrow being sunny is 5/6 (simulate with dice). What is the long term probability of a day being sunny or not?
- Simulate with 30 throws of dice and see the answer.
Aha! So we can get 50:50 probability even when events are not independent. These are called Markov Chains.
Let's try to find a simple way to solve these using linear equations
- For the first example, If a and b represent long term stable probabilities, then successive turns should yield the same probability. Hence a = 0.5a+0.25b and b = 0.5a+0.75b. We also know that a+b=1. Solve for it
- Answer: 1/3 and 2/3
- For the second example, r = 5/6r+1/6s and s = 5/6s+1/6r
- Answer: 1/2 and 1/2
- How would you extend it to more states?
- Essentially, we can transition from any state to any state, including itself, with given probabilities (totaling to 1 our of each state). Then we run the model long enough, and we get stable state probabilities.
- Sometimes, Markov Chains may not converge to a unique solution. For example, if you have a cycle of transitions and nothing else ("periodic" chains)
So why is this interesting - Monopoly!
How does Monopoly work? Can we think of it as probability of landing on a given square? What does that depend on?
- Previous square
- Dice roll value (we already know that for roll of two dice, what are the probabilities of each value) - Revisit
- What else?
- Chance cards/ Community cards
- 3 doubles take you to Jail
So if we tell you where you are currently, you can find out the probability of where you land up next. Just like in above examples, we had two states, here we have 40 states (if we incorporate the doubles and other cards all into the probability computation).
What will happen if we now solve it over large number of throws?
- It should give us the chances of being on any given square
- Do you expect chances of being on a given square to be the same/ different?
Lets see - this is where we can be with 2000 rolls (http://bewersdorff-online.de/amonopoly/monopoly_s.htm)
.png)
And this is where we land up after a long set of moves - What can you deduce from it? (Look at Jail and Just Visiting together. Don't bother about the colors yet)
.png)
If you were playing Monopoly, how would you incorporate this into your gameplay?
- What properties would you buy?
- Chance of opponent landing there?
- Price versus rent?
- What groups of properties are most valuable?
- Others?
Instructor Notes: Let kids think about the questions above, and get to the criteria - For example: one should buy properties that have the highest earning potential in relation to their cost. Or breakeven point. Or highest chances of an opponent coming to it.
Lets see some of the results:
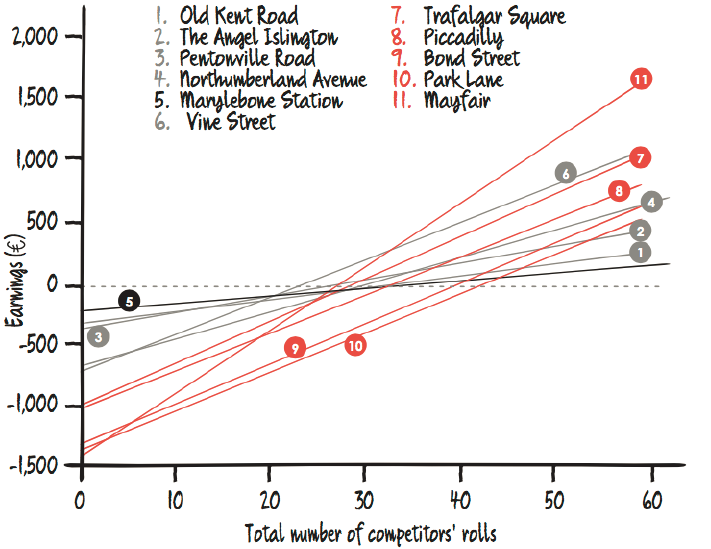
And for color sets:
.png)
And to Practical Stuff - Foundations of Google Pagerank
Google ranks all web pages as per pagerank. Lets see the basis of this:
- Let there be N web pages. Each webpage (j) has k outgoing links
- Lets construct a probability graph of going from one webpage to another, assuming the user can take any of the outgoing links with equal probability
- Then the probability of a person being on a particular webpage is its pagerank - it denotes that this page is linked from a lot of other pages, and hence must be important
Time permitting, lets calculate relative ranks of the pages in following web.
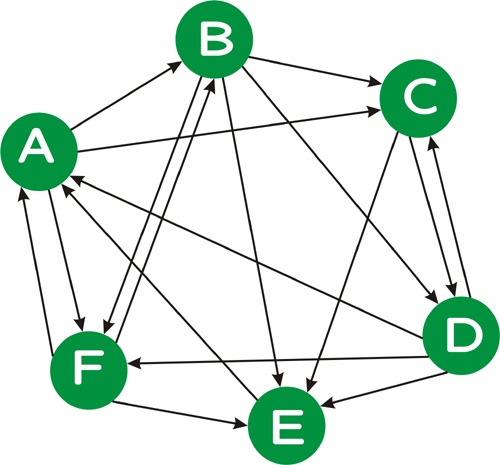
Google also solves the "dead end" problem, by taking a probability that at any point, the surfer may just quit random navigation and type in one of the pages in URL (effectively "jump").
(See Excel Sheet Pagerank Attached)
Homework
Think about one more game that you like, which can be modeled as Markov Chain. Think about what "states" represent, and how you would create a transition diagram. Think about the elements you would take into account to assign probabilities to transition. Finally, on a simplistic version, try to find probabilities of outcomes. What outcomes are important in your game?
References: